Εμβαδον Τραπεζιου Τυπος Σχημα

Εμβαδόν Τραπεζίου Υπολογισμός Τύπος

από

Τραπέζιο είναι το γεωμετρικό σχήμα που έχει 4 ευθείες πλευρές, δύο από τις οποίες είναι παράλληλες.

Οι παράλληλες ευθείες είναι επίσης γνωστές ως βάσεις , ενώ οι άλλες δύο είναι γνωστές ως σκέλη του τραπεζίου

Η κάθετη απόσταση μεταξύ των παραλλήλων καλείται ύψος του τραπεζίου.

Γρήγορη Μετάβαση : Κομπιουτεράκι για Υπολογισμό

Τύπος Εμβαδού Τραπεζίου και Απόδειξη

Το εμβαδόν του τραπεζίου δίνεται από τον τύπο

Εμβαδόν = ½ • υ • (α + β)

όπου υ η κάθετη απόσταση ανάμεσα στις παράλληλες (ύψος) και α , β το μήκος των παραλλήλων.

 

Απόδειξη του Τύπου 1ος τρόπος

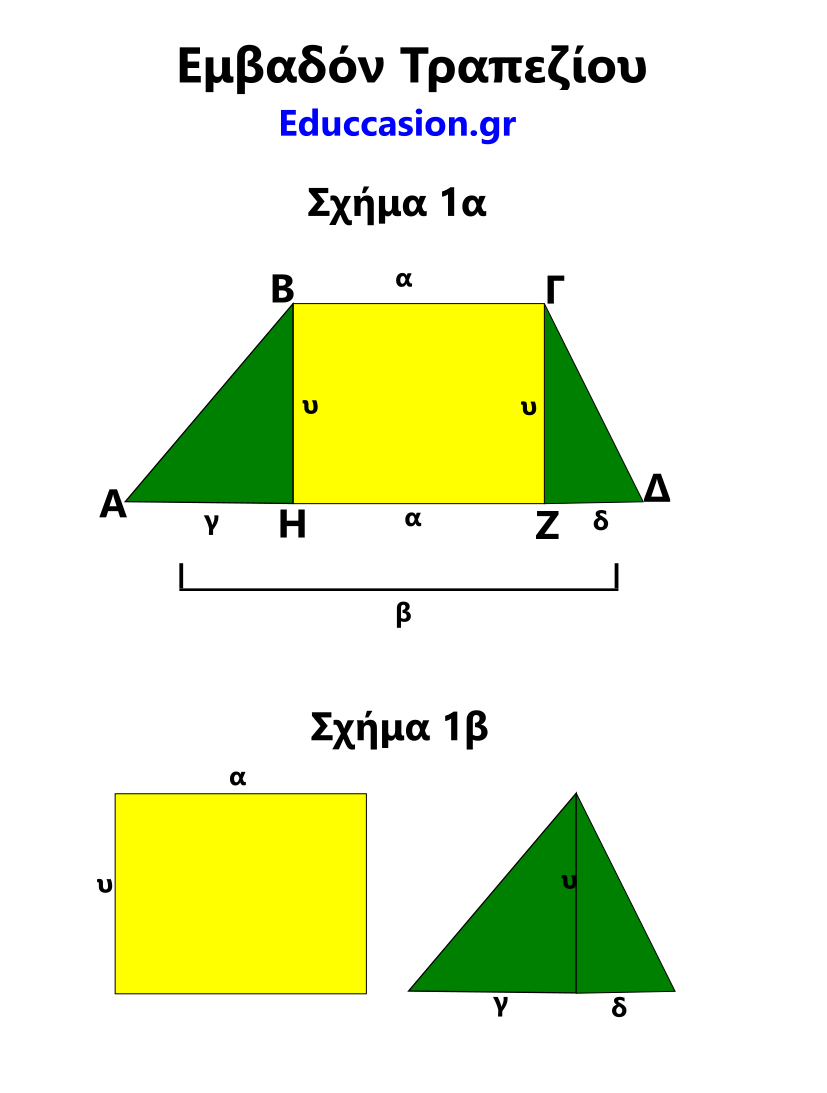
Έστω τραπέζιο ΑΒΓΔ με παράλληλες τις ΒΓ και ΑΔ με μήκος α και β αντίστοιχα όπως φαίνεται στο Σχήμα 1α .

Για να βρούμε το εμβαδόν μπορούμε να χωρίσουμε το Σχήμα 1α στο παραλληλόγραμμο ΒΓΖΗ με μήκος παραλλήλων α και β και στα ισοϋψή ορθογώνια τρίγωνα ΑΒΗ και ΓΔΖ με μήκος βάσης γ και δ αντίστοιχα . Παρατηρούμε ότι β= α + γ + δ

Προσθέτουμε το Εμβαδόν Ε των επιμέρους σχημάτων και έχουμε :

Εμβαδόν = Ε(ΒΓΖΗ) + Ε(ΑΒΗ) + Ε(ΓΔΖ) = (υα) + (½υγ)  +  (½υδ) =

= (2 • ½ υα) + (½ υ γ)  +  (½υδ) =

= ½ υ(2α + γ + δ) = ½ υ(α + α + γ + δ) επειδή όμως β= α + γ + δ θα έχουμε :

Εμβαδόν = ½ υ(α + β) 

 

Εμβαδόν Τραπεζίου Απόδειξη Τύπου με δύο τρίγωνα
Πως αποδεικνύεται ο τύπος του εμβαδού τραπεζίου με τους τρόπους των δύο τριγώνων. Στο Σχήμα 1α αθροίζονται τα εμβαδά των δύο τριγώνων με αυτό του ορθογωνίου παραλληλόγραμμου. Στο Σχήμα 1β μετά από την ένωση των δύο τριγώνων προσθέτουμε πάλι με το ορθογώνιο παραλληλόγραμμο.

 

Απόδειξη του Τύπου 2ος τρόπος

Εφόσον τα δύο τρίγωνα ΑΒΗ και ΓΔΖ είναι ισοϋψή σχηματίζουμε ένα νέο νοητό τρίγωνο (Σχήμα 1β) με ύψος υ ίσο με το ύψος του τραπεζίου και βάση ίση με το άθροισμα των βάσεων γ + δ των δύο τριγώνων.

Για να υπολογίσουμε το εμβαδόν του τραπεζίου προσθέτουμε την επιφάνεια του παραλληλόγραμμου και την επιφάνεια του νέου τριγώνου.

Εμβαδόν = υα + ½υ(γ+δ) = 2½υα + ½υ(γ+δ) = ½υ(2α + γ + δ) = ½υ(α + α + γ + δ)

Από το (Σχήμα 1α) γνωρίζουμε ότι β = α + γ + δ επομένως :

Εμβαδόν = ½ υ(α + β) 

Απόδειξη του Τύπου 3ος τρόπος

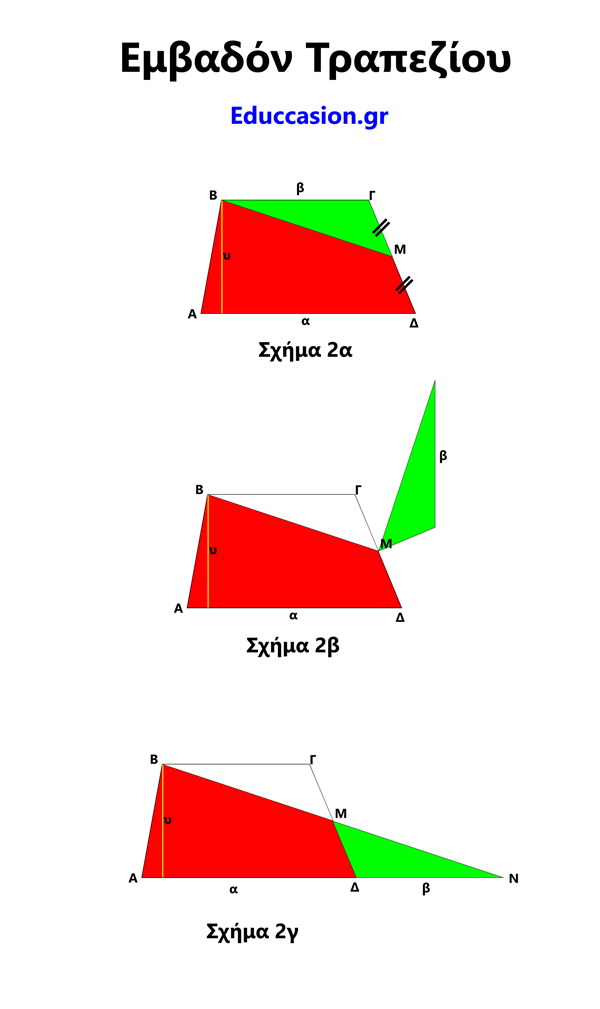
Έστω τραπέζιο ΑΒΓΔ (Σχήμα 2α) με παράλληλες πλευρές α και β και το σημείο Μ που βρίσκεται στη μέση της πλευράς ΓΔ. Έστω ότι στο σημείο Μ περιστρέφουμε (Σχήμα 2β) δεξιόστροφα το τρίγωνο ΒΓΜ ώστε η πλευρά ΓΜ να εφάπτεται στο ισομήκες τμήμα του τραπεζίου ΜΔ.

Προκύπτει τώρα ένα νέο τρίγωνο (Σχήμα 2γ) ΑΒΝ με βάση ίση με α+β και ύψος ίσο με το ύψος υ του παλιού τραπεζίου.

Το Εμβαδόν του αρχικού τραπεζίου θα ισούται με το εμβαδόν του νέου τριγώνου του σχήματος 2γ οπότε :

Εμβαδόν = ½ • βάση • ύψος <=>Εμβαδόν = ½(α + β)υ

Εμβαδόν Τραπεζίου Απόδειξη Τύπου με Μετασχηματισμό σε Τρίγωνο
Στο Σχήμα 2α σχηματίζουμε εσωτερικά στο τραπέζιο τρίγωνο του οποίου η μία γωνία χωρίζει το ένα σκέλος του τραπεζίου σε δύο ίσα μέρη. Στη συνέχεια στα σχήματα 2β και 2γ το τρίγωνο περιστρέφεται ώστε να μετατρέψει το τραπέζιο σε τρίγωνο. Τέλος υπολογίζουμε το εμβαδόν του νέου τριγώνου και αποδεικνύουμε τον τύπο.

 

Απόδειξη του Τύπου 4ος τρόπος

Έστω τραπέζιο ΑΒΓΔ με παράλληλες πλευρές α και β και ύψος υ. Δημιουργούμε ένα νέο τραπέζιο αντιστρέφοντας το αρχικό κατά 180 μοίρες και τα ενώνουμε ώστε να δημιουργηθεί παραλληλόγραμμο.

Εμβαδόν Τραπεζίου Απόδειξη Τύπου με χρήση Παραλληλόγραμμου
Εύρεση Εμβαδού Τραπεζίου με περιστροφή κατά 180 μοίρες και ένωση του νέου σχήματος με το αρχικό ώστε να δημιουργηθεί παραλληλόγραμμο. Στη συνέχεια υπολογίζουμε το εμβαδόν του παραλληλόγραμμου.

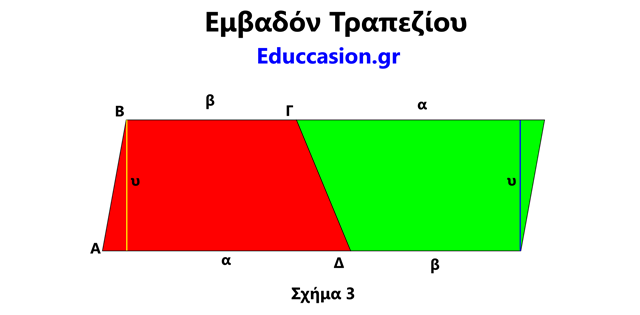
Από το Σχήμα 3 βλέπουμε ότι μπορούμε να υπολογίσουμε την επιφάνεια του αρχικού τραπεζίου βρίσκοντας το εμβαδόν του παραλληλόγραμμου και διαιρώντας δια 2 :

Εμβαδόν Τραπεζίου = ½(Εμβαδόν Παραλληλόγραμμου) = ½ (α + β) υ

Υπολογισμός Εμβαδού με το Κομπιουτεράκι

Μετάβαση στην εφαρμογή για υπολογισμό